This page was written by Michael Lueckheide ’13
The Quantum Dots
Quantum dots are nanoparticles of semiconducting material.
Data Modeling (Diffraction Patterns)
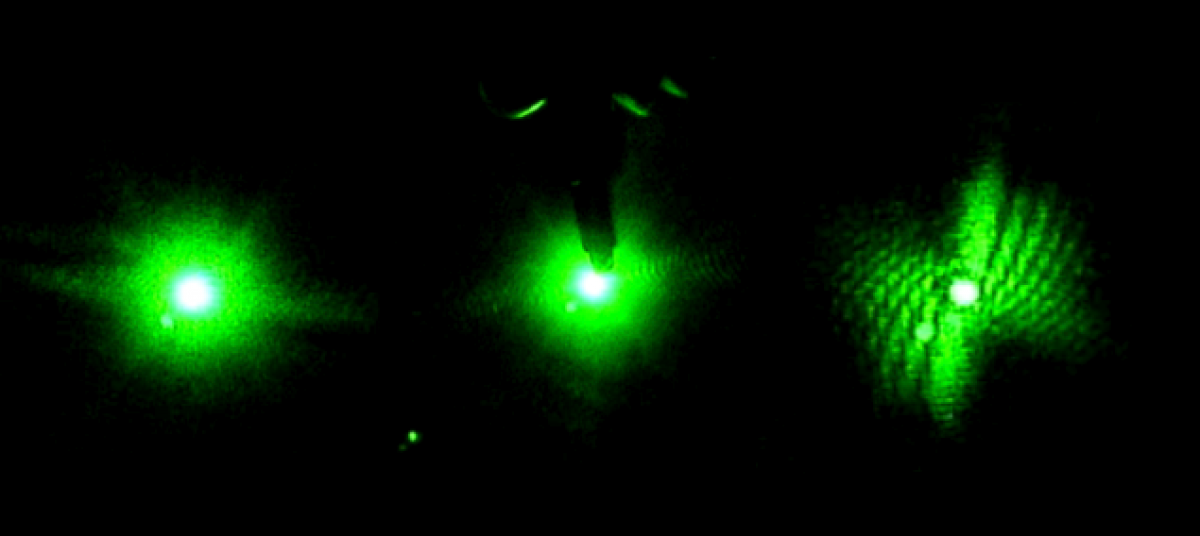
The first step in the quantum dots project was to use the Fast Fourier Transform (FFT) to model the diffraction patterns created by a random arrangement of dots in Mathematica.
-
- A set of dots with randomly generated positions and diameters. The actual size of this image is 1024 x 1024.
Taking the FFT of this image yields the following diffraction pattern.
- A diffraction pattern created by the random set of dots.
The resolution of the diffraction pattern is governed by the matrix that represents the original dot pattern. Each white pixel in the dots is represented by a one in the matrix, and the black background pixels are zeros. The more zeros the surround the ones in the matrix, the better the resolution of the FFT will be. To add more zeros to the matrix, an image with more background was required. To this end, a screenshot of the dot pattern was taken and opened in Preview. The background of the display window was turned black to match the dots’ background. Then a 1024 x 1024 screenshot of the dots was taken that had much more black background than before. It was this, new screenshot that was imported into Mathematica to transform with an FFT.