The data generated in my project consisted of position data for the path of a squash ball in motion in the spatial context of a squash court. Additional important generated data included the velocity of the ball (in 3-dimensions) at any given time. Euler’s method was a relatively practical numerical method, as it made calculating the position at each step of dt (which was imperative in the animation aspect of the project) a simple matter of using the position and velocity information from the previous time step.

Some difficulty arose in attempting to achieve a smooth animation, due partly to computational time. Ultimately the solution for animating the path of the squash balls necessitated creating matrices for the position of the ball in each dimension in Cartesian coordinates. After this, the comet3 function was used to animate the plot, as it the head of the comet nicely approximated the shape of a ball, and the tail was very useful in showing the entire path of the ball from its initial position.

In the end, my goals for the project had to be altered slightly, as attaining the user-friendly inputs that I had wanted proved to be a complicated task. I had initially hoped that the finished product would allow for a user to input some initial velocity using the arrow keys. Ideally the user would hold down some combination of the arrow keys for some amount of time, and then press the spacebar to initialize the loop and set the ball in motion. Based on the amount of time each direction arrow had been pressed, the ball would be imparted with a corresponding initial velocity. However, unfortunately Matlab’s capabilities to not allow for the reading of key presses without the use of user-generated GUI’s. Given that my understanding remains relatively basic, I had to scrap my dreams of user-interaction with the model.

Though the ultimate goal of my script was an educational experience for the user, writing the script was a learning experience in itself. I had previously modeled some colliding pendulums in Matlab, and I drew on this code in scripting the ball-to-wall collisions, and subsequently the resultant velocities of the ball was an easy task. In the early draft of my code I encountered some problems, as certain initial velocities seemed to result in the ball getting stuck inside the walls – an obviously undesirable result due to its physical improbability. Having encountered a similar issue in my colliding pendulums code, I knew that the problem had something to do with the script not checking on the position of the ball often enough, due to the time step, ‘dt’, being too large. While this was part of the problem, the larger source of the issue was the fact that, once beyond the wall, the ball’s velocity was rapidly decreasing, as the script believed that it was continuously colliding with the wall. In the end the fix was relatively simple: if the ball passes beyond the wall, reset the balls position so that it is at the wall again. Though simplistic, this is a powerful idea in the context of computational methods. If having a variable reach a target value is desirable for your simulation or simplifies the problem, just check that the variable comes within a reasonable range and set it to the target value.

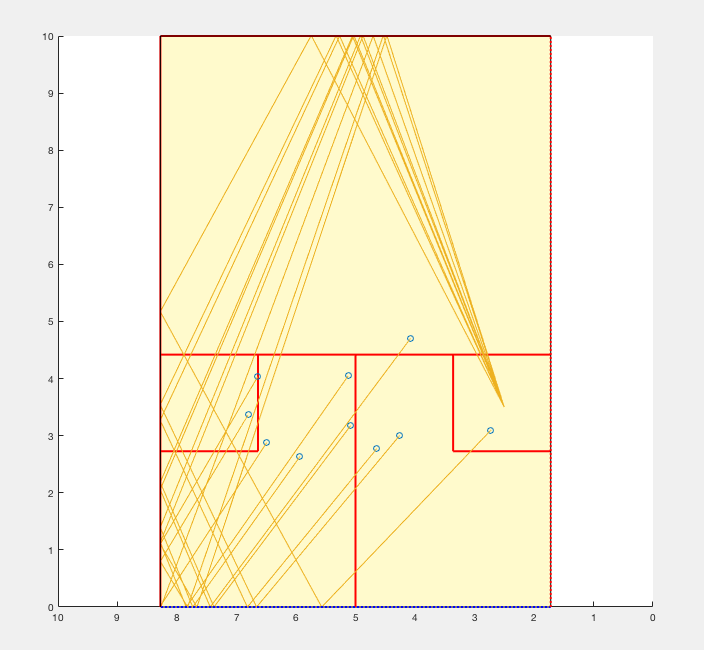
I was surprised to note how relatively close to the front and right wall many of the balls ended up. This was most likely due to the fact that my expectations came from having played squash. When returning the serve, the goal is to hit the ball back before it bounces twice, therefore if you have watched to ball until it stops rolling (as the script does), you have long since lost the point. It was interesting to confirm that the majority of serves bounce twice within the confines of the larger box in the back left of the court (makes up about a quarter of the floor) which verified my own experience that almost all serves are returned from the back left of the court. Though these results seem quite inconsequential, the objective of the script is an educational experience, so these observations can be read as positive outcomes.

The goal of my script was entirely focused on user experience. Consequently, the product of the script was not heavy on calculated results. The main idea was for users to be able to gain an intuition for the flight path of a squash serve without ever having played, or even seen the sport being played before. On the other hand, it may have been interesting to take the project in a more numerical-result-driven direction. For instance, a comparison of the initial angle of the ball with the final angle would have made for an interesting discussion. Having run through the script a number of times, and therefore seen at least a hundred individual ball paths fully plotted, a distinction between the serves that struck the side-wall before the back-wall, and those that did the opposite definitely emerged. Quantifying this difference could potentially be illuminating. Another question that might be considered concerns the balls that hit the side-wall and back-wall simultaneously. How would these corner cases (pun intended) show up in the data? If I were to modify the script to accomplish this, the most important change would be to increase the number of iterations from ten into the hundreds or even thousands. This would almost certainly necessitate abandoning the full animation of the flight path, and focusing instead on the location of the ball’s second bounce on the floor (when, according to the rules of squash, the point has ended).

If I were to instead expand my project to expand the user’s experience and fully embrace the educational aspect of the project, I would certainly want to solve the problem of more interactive user input. Allowing the user to control the velocity would allow them to develop a feel for the serve without ever having stepped on a court, whereas the project in its current state relegates the user to the role of an observer, rather than an active participant. Ideally the project could be taken beyond the confines of a serve, and allow the user to control a player that plays out a full point, perhaps against a computer-controlled player. This would potentially require quite complex user input capabilities (for position of the player and velocity and direction of each hit) and would also necessitate a method of plotting that was instantaneous. A more simplistic full-point simulation could also be created by creating additional collision areas that represent swinging rackets at various locations the court, so that a ball that happened to reach that position would be imparted with some new velocity and direction.

Sources:

<http://www.worldsquash.org/ws/resources/court-construction>

<http://www.worldsquash.org/ws/resources/rackets-balls/racket-ball-specifications>