The project focuses on creating a visual model displaying the random movement of an atom through various structures. The program models and compares the substitutional diffusion of atoms through a two-dimensional fractal and three three-dimensional types of crystal lattices. The models created are most useful in visually understanding the process of diffusion and the impact of the structure in determining the process of diffusion. These could be used in any class that discusses basic crystallography and solid state physics to help visualize the processes within the structures.
Background:
Atomic diffusion is the random thermal movement of atoms through a solid. In crystals, atomic diffusion can occur through interstitial or substitutional means. Interstitial diffusion refers to when atoms move in between the lattice points of a crystal. The atoms have a slightly greater freedom of movement, as the only conditions are that there is an unoccupied location adjacent to the particle and that the particle has enough thermal energy to diffuse there. Substitutional diffusion, which is the focus of this project, occurs when an atom takes the place of an atom in the lattice. The atom can thus move around the lattice by switching places with other atoms.
Crystal lattices are the periodic repetition of a structure, where the base unit is known as a unit cell. The unit cell of a lattice can be determined based on the locations of the fewest lattice points needed to repeat the structure. Thus, for a simple cubic lattice, with one lattice point at each edge of a cube, the lattice can be described by the point at (0,0,0). With repetition, this point repeated in each direction every length a (the lattice constant) will create a simple cubic lattice. A body-centered cubic lattice is a simple cubic lattice with an extra lattice point in the center of the cube. It can be described by the two points (0,0,0) and (1/2,1/2,1/2). In comparison, a diamond lattice is more complicated. Found commonly in diamond itself and in semiconductors such as silicon, a diamond cubic lattice requires eight lattice points to repeat the structure. These points are located at (0,0,0), (0,1/2,1/2), (1/2,0,1/2), (1/2,1/2,0), (3/4,3/4,3/4), (3/4,1/4,1/4), (1/4,3/4,1/4), (1/4,1/4,3/4).
Model:
The program is separated into two sections. The first section creates a fractal by plotting the real and complex parts of the solutions to an iterated complex equation against each other. Several particles are placed inside the fractal and consecutively allowed to randomly walk in two dimensions. The fractal acts as a wall for the particle’s movement. The program limits the particle’s movement by either stopping the particle from moving within a certain radius of the fractal’s edge, or by resetting the particle to the origin. The particle’s motion is plotted and tracked for clarity of understanding the motion of the particle. The section demonstrates diffusion by random walk in a large section of a medium, limited by boundaries.
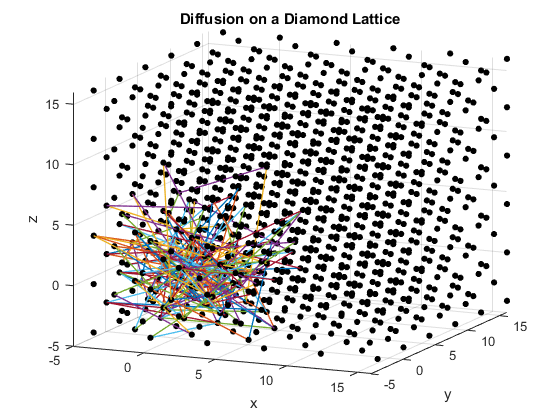
The second section of the program plots a simple cubic lattice, a body-centered cubic lattice, and a diamond cubic lattice. A particle is placed at the origin of each plot and allowed to move randomly to adjacent lattice points. The lattice constant is set to be four, and each particle can move a distance of at most magnitude five per time step. This allows the particle to move to any nearby point via substitutional diffusion. The particles’ movement is plotted for their first 200 steps.
Several key assumptions are made by the program. First and foremost, all adjacent points are considered equally likely locations for the particle to diffuse to. This assumes that all directions and distances up to a distance magnitude 5 away are equally viable for the particle’s movement, and that the particle does not lose energy over the course of diffusion. It also assumes that all atoms in the lattice, apart from the additional particle (shown in red) are the same element, isotope, and chemical properties. Secondly, it is assumed that the new atom can easily displace the previous atoms. These assumptions allow the program to easily model the movement of the atom for visualization purposes.
Data:
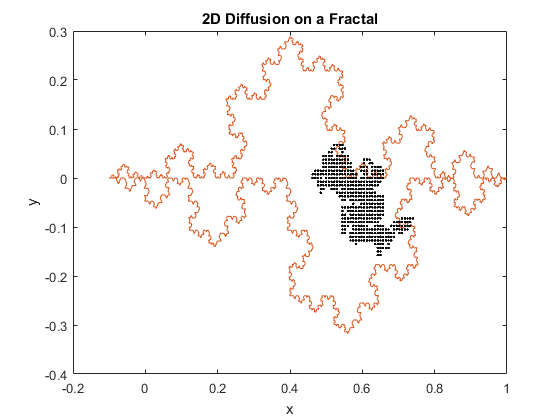
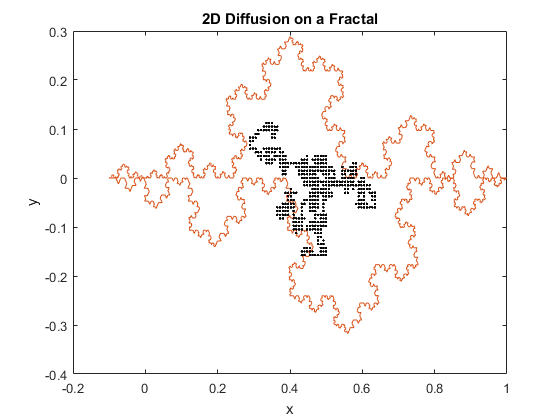
Figures 1(a) and (b): 2D diffusion of particles on a fractal.
The above figures represent two iterations of 2D diffusion on a fractal. The fractal is plotted in red, while the movement of the particles are plotted with one dot corresponding to one step taken by a particle. The figures show the range of the motion of the particles. While the program generally confines the particle to the interior of the fractal, as can be seen in both figures the particles can be capable of diffusing past the fractal’s boundary. Diffusion across a boundary can occur when there is a lower activation energy for diffusion and when there is a defect or open lattice point on the other side of the boundary.
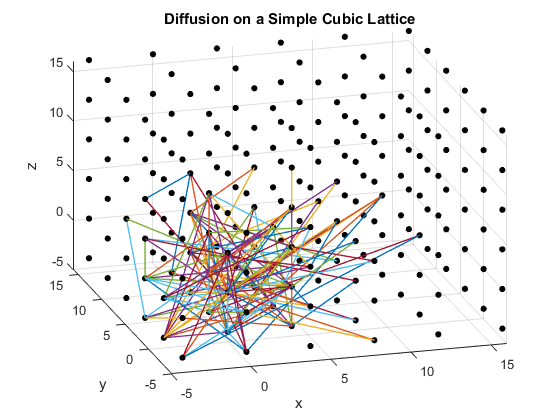
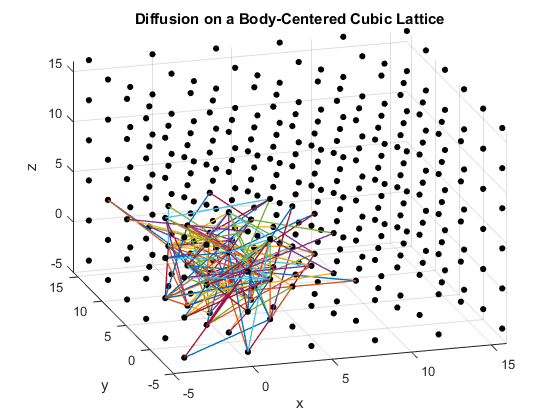
Figures 2(a), (b) and (c): 3D diffusion on various crystal lattices.
The particles diffuse through the lattices as intended. The particle in the simple cubic lattice travels farther, while the particle in the body-centered cubic lattice remains slightly more compact in its diffusion. This follows from the probability of motion and the assumptions that were made in the program. As a body-centered cubic lattice has more lattice points close to the original, there is a slightly higher probability that the particle will remain close to the original location. This effect is small, as the particle has only one additional lattice point per unit cell that it can reach. Similarly, the path of the particle in the diamond cubic lattice displays compactness close to the origin. As before, this is due to a small increase in the probability that the random motion of the particle will go to a nearby lattice point, as there are significantly more lattice points per unit cell in the diamond crystal lattice than in the simple cubic or body centered cubic lattices.
The model is perhaps most effective in its ability to rotate or to be moved in three dimensions while the particle is diffusing. The model can also display the diffusion in each of the two-dimensional views. The ability to manipulate the view of these diffusions allow a greater understanding and intuition of lattices and the motion of particles within lattices.
The model does not consider multiple particles diffusing at once, more complex atomic alignments within the lattice, or diffusion methods other than substitutional. The program also struggles to effectively model large crystal structures, as such structures use substantial amounts of memory. However, for smaller scale models or for varying time scales, the program and its models are very effective.
Conclusion
The program effectively plots three-dimensional random substitutional diffusion on three lattice structures. It similarly plots two-dimensional random diffusion on a fractal structure. The fractal confines most particles to within its bounds and explanations are offered of cases where diffusion can be seen to cross boundaries. The four models can be used as educational tools, increasing knowledge and intuition for students about diffusion in solid-state systems.
Sources
[1] Giordano, Nicholas J. Computational Physics. Upper Saddle River, NJ: Prentice Hall, 1997. Print.
[2] Kittel, Charles. Introduction to Solid State Physics. New York: Wiley, 1986. Print.
[3] Shaw, D. Atomic Diffusion in Semiconductors. London: Plenum, 1973. Google Books. Web.