Electric Double-Layer Capacitors

Electric Double-Layer Capacitors (EDLC), variously referred to by manufacturers in promotional literature as supercapacitors or ultracapacitors, store electrical charge in a double layer at the interface between a carbon electrode and an electrolyte.

In a conventional capacitor energy is stored by the removal of charge carriers, typically electrons, from one metal plate and depositing them on another. This charge separation creates a potential between the two plates, which can be harnessed in an external circuit. The total energy stored in this fashion is proportional to both the amount of charge stored and the potential between the plates. The amount of charge stored is essentially a function of size and the material properties of the plates, while the potential between the plates is limited by dielectric breakdown  of the substance separating the plates. Different materials sandwiched between the plates to separate them result in different voltages to be stored. Optimizing the material leads to higher energy densities for any given size of capacitor.

V = V₊ – V_– = ∫ E·dl

In a parallel-plate capacitor consisting of tow metal surfaces of area A, a distance d apart, and +Q on the top and -Q on the bottom, then we know that the electric field (which is uniform and constant between two plates) is E = Q / Aɛ and the potential difference between the plates is there 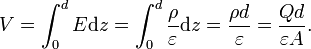. Hence . And the total energy stored in the capacitor is :

Networks of capacitors:

For capacitors in parallel: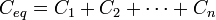

For capacitors in series:

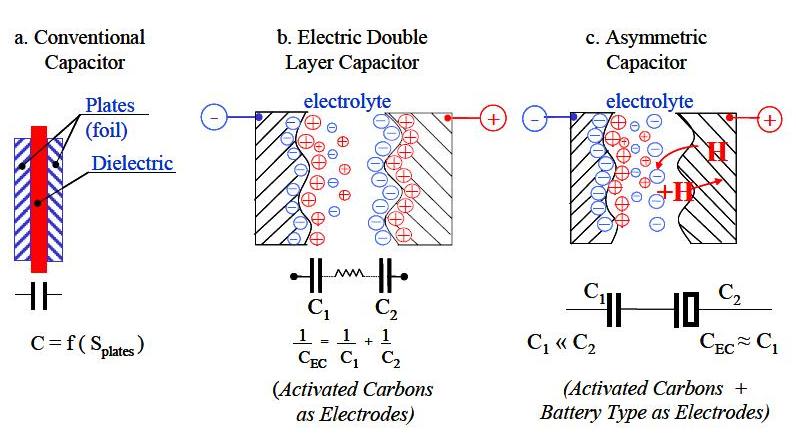
Electric double layer capacitors have electric charges oriented at the boundary of electrolyte and electrodes in what is called the “electric double layer.  EDLCs do not have a conventional dielectric. Rather than two separate plates separated by an intervening substance, these capacitors use “plates” that are in fact two layers of the same substrate, and their electrical properties, the so-called “electrical double layer”, result in the effective separation of charge despite the vanishingly thin (on the order of nanometers) physical separation of the layers. The lack of need for a bulky layer of dielectric permits the packing of “plates” with much larger surface area into a given size, resulting in extraordinarily high capacitances in practical-sized packages. In addition, EDLC differs from rechargeable batteries, not causing chemical reaction, with surface of activated carbon with energy accumulation by ionic physical attachment only.

Because of the high internal surface area of the nanoporous carbon electrode material and the nanosize thickness of the double layer, electric double-layer capacitors have a much higher energy density that is several orders of magnitude greater than those of electrolytic and electrostatic capacitors: a typical D-cell sized electrolytic capacitor will have a capacitance in the range of tens of millifarads. The same size electric double-layer capacitor would have a capacitance of several farads, an improvement of about two or three orders of magnitude in capacitance, but usually at a lower working voltage. This is an enabling technology by which previously unattainable capacitance density is coupled with essentially unlimited charge/discharge cycle life. ECs possess high power density but low energy density relative to batteries; therefore, they serve a functional purpose between conventional capacitors and batteries.

Here  is a sample of my modeling: The electric field vs. Charge in different capacitors. This would be further developed when I look into the different materials used for the Electric Double Layer Capacitor (Activated carbon, graphene, carbon nanotubes and certain conductive polymers, or carbon aerogels, are practical for supercapacitors.)

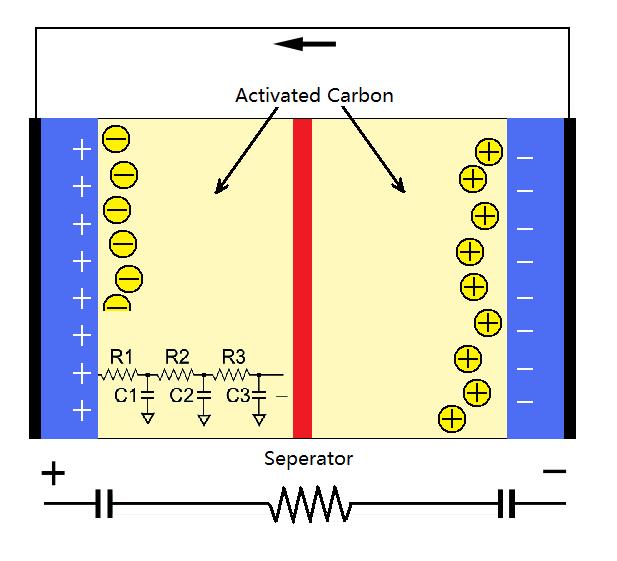
Here we use the de Levie model: de Levie showed that the impedance of a single pore of length l had an impedance given by Z_PORE.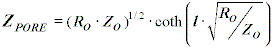 

This equation holds for any type of interfacial impedance as long as the interfacial impedance does not depend upon the position in the pore.

For a small length of the pore, dx, the electrolyte resistance, dR, and interfacial impedance, dZ are given by the equations, below.  The radius of the pore is r cm, and the resistivity of the electrolyte is ohm-cm. Zo is the impedance at the pore wall-electrolyte interface for a unit length of pore.

If all of the n pores in an electrode are identical (radius r and length l) the equation for Z_PORE can be used to obtain the total experimental electrode impedance if the interfacial impedance ( Z_IF ) is known

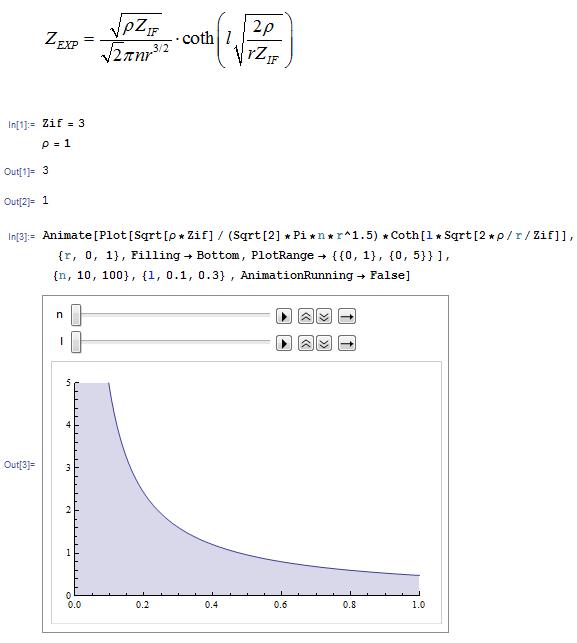
[Here is the Mathematica Notebook.]

Activated charcoal has some problems as the holes in the charcoal are often smaller than the charge carriers  – especially when surrounded by solvent molecules. A possible solution is to replace activated carbon/charcoal with carbon nanotubes.

Here are some of the advantages of the Electric Double Layer Capacitor:

• With low degradation, multimillion cycles of charge-discharge is possible.
• With a high power density, rapid (high current) charge-discharge is possible.
• With a high charge-discharge efficiency, an output efficiency of over 95% with a power density 1kW/kg is obtained.
• Environmentally friendly without using heavy metal for its structure material.
• High in safety during abnormal time, and no malfunction occurs due to short circulation.

(Picture Source: Wikipedia)

Here is a video of a recent development of the Electric Double Layer Capacitor:

Here is another video of a flashlight using supercapacitors:

_________________________________________________________________________________

4/20/10

I had a lot of fun with the Rectangular Waveguide in TM Mode in Mathemtaica.

Here is the link to the file.

_________________________________________________________________________________

3/29/10

Here is the awesome wave file.

_________________________________________________________________________________

3/21/10

Summary of Journal:

At first I embrace the idea of keeping a physics diary as peculiar and innovative, but soon I find this quite helpful in my thinking and studying process.
Taking a 300 level Physics course in electromagnetism is a challenge that I am extremely enthusiastic about. Having taken PHYS-240 Electromagnetism I and multivariable calculus, I believe that I am academically prepared to take on this challenge. However, in the beginning of the semester I still find the material quite difficult: for one thing I indeed forgot some of the things that I learned in the previous electromagnetism class after the winter break (maybe due to all the roller coaster rides I took in Disneyworld); for another, the study of dielectrics (I am curious why people don’t just use the word ‘insulators’) is far more complicated in nature when compared with that of conductors.
The revision of the Maxwell’s equations and the Lorentz force law is a wonderful and helpful way to start the semester, as it brought back the old memories and knowledge. In the second week we, a quite small and intimate group of students, moved on to take a close look at the polarization in dielectric materials. At one point I was confused about the p (atomic polarizability) and P (polarizations or the dipole moment per unit volume), especially because they are both vectors, but later learned the big difference between the two. Bound charge was another slightly perplexing concept, but the book is helpful by offering a physical interpretation of bound charges and a detailed description of free charge. The Gauss’s law for the electric displacement is useful in simplifying many complicated problems, but the parallel is ‘deceptive’. Such deceptive parallels are abundant in physics, and I have a lot of interests in them. Another example is the shape of the electric field at the interface between one linear dielectric and another (no free charge at the boundary) reminds me of Snell’s law in optics. Although there are big differences between them, this made me think about the nature of light and a series of models related.
Finally in this chapter I am very interested in the application of the dielectric systems, particularly dielectric filled capacitors and the energy stored dielectric systems. This interest recorded in the diary eventually lead to my decision on making a blog based on modeling the energy stored in capacitors (with different dielectric constants, geometric shapes, possibly parallel or series of capacitors).

_________________________________________________________________________________

3/16/10

We ran into this beautiful wedding in Santo Domingo Church in Oaxaca, Mexico.

Well, the day after I recovered from food poisoning in Mexico, I had to be on a bus going from San Cristobal to Palenque. While I was tracking the slowly motion of the blue dot on the GPS, I couldn’t help but thinking about the GPS system. Well, how many satellites do we need for locating a point? How does the GPS determine the north and south on the phone?

Three satellites might seem enough to solve for position, since space has three dimensions and a position on the Earth’s surface can be assumed. However, even a very small clock error multiplied by the very large speed of light[20]—the speed at which satellite signals propagate—results in a large positional error. Therefore receivers use four or more satellites to solve for the receiver’s location and time. The very accurately computed time is effectively hidden by most GPS applications, which use only the location. A few specialized GPS applications do however use the time; these include time transfer, traffic signal timing, and synchronization of cell phone base stations. (Wikipedia) On my phone, I usually find it connected to six satellites when the GPS is working properly.

_________________________________________________________________________________

3/20/10

A Update on the blog, here is a video about ultra capacitor flashlight

_________________________________________________________________________________

Blog Proposal

The topic of my project is Energy Stored in Supercapacitors. Capacitors are widely used in our lives. When a potential difference exists across the conductors, an electric field is present in the dielectric, which stores energy and produces a force between the conductors.  The model makes a study of the Supercapacitors, or electric double-layer capacitors. They have unusually high energy density when compared to common capacitors, which brings certain advantages and disadvantages.  The software Mathematica would be used to model the different geometric shapes of the dielectric capacitors and capacitors filled with materials with different dielectric constants. I also expect to generate a Mircrosoft Excel sheet comparing the energy stored in different capacitors.

UPDATED: Stored Energy for Different Dielectric Constants and Shapes (Possible take a look at ultra capactiors) with Mathematica

http://en.wikipedia.org/wiki/Electric_double-layer_capacitor

_________________________________________________________________________________

2/16/2010

There is this stunning similarity between Snell’s law and this electric field. The Mathematica file is here. Please enable dynamic when you open the file so that you could play with different θ or R values. The default value for R, which is the ratio of the dielectric constants, is 0.5.

_________________________________________________________________________________

2/8/2010

Mathematica work sheet on vector fields with Griffiths 4.10 is here. I find it a big advantage to use SphericalPlot3D to show the polarization inside the sphere.