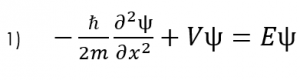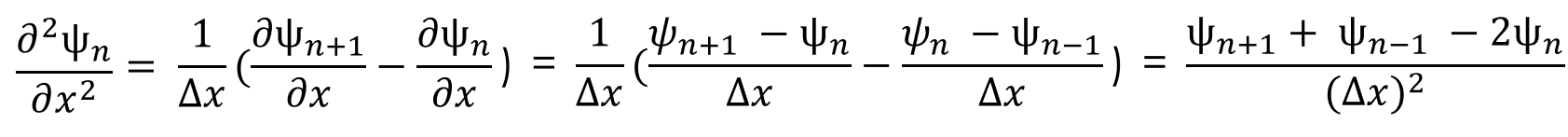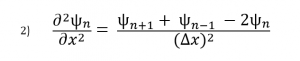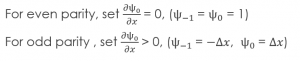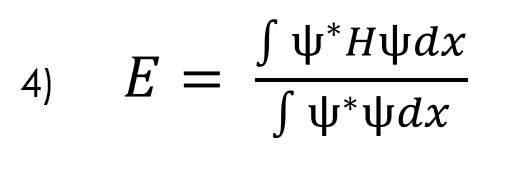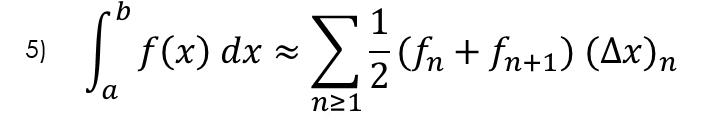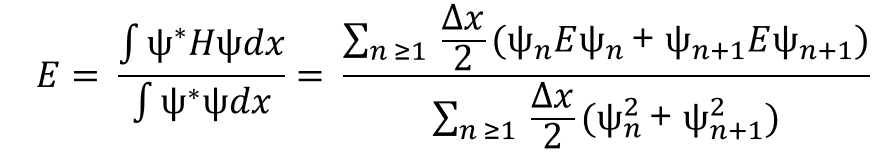In this post I will attempt to teach the reader two computational methods that are commonly used to analyse quantum systems. These methods are known as the matching method and the Monte Carlo method. These methods each have their own advantages and disadvantages in various scenarios which is why I believe it would be useful to the reader to have both of these methods under their tool belt.

The basis of all of our calculations in a quantum system will typically be based on the time independent Schrödinger equation, so lets first analyse this equation to see how it can be used computationally.

We can approximate the double partial derivative of the wave function as:

Now that we have an equation for the double partial derivative, we can enter this back into the Schrödinger equation and rearrange the terms in the following way:

We now have an equation that allows us to compute any wavefunction given an energy and potential.

Matching Method

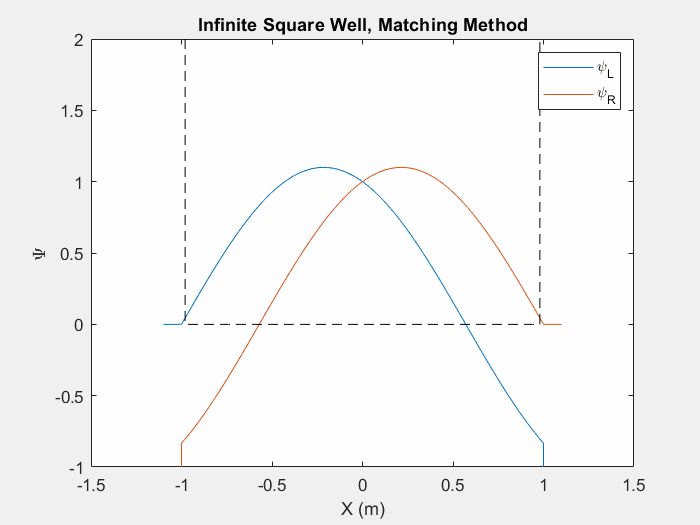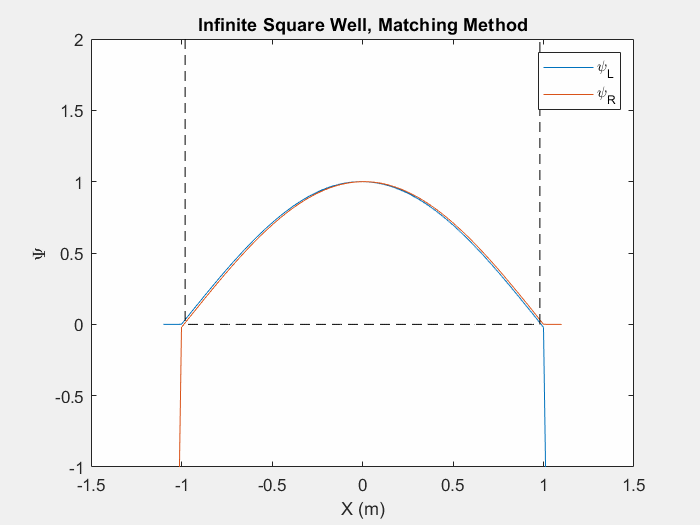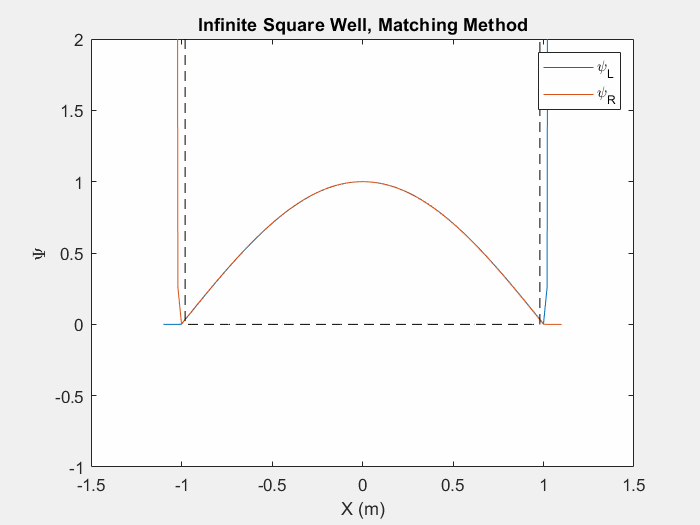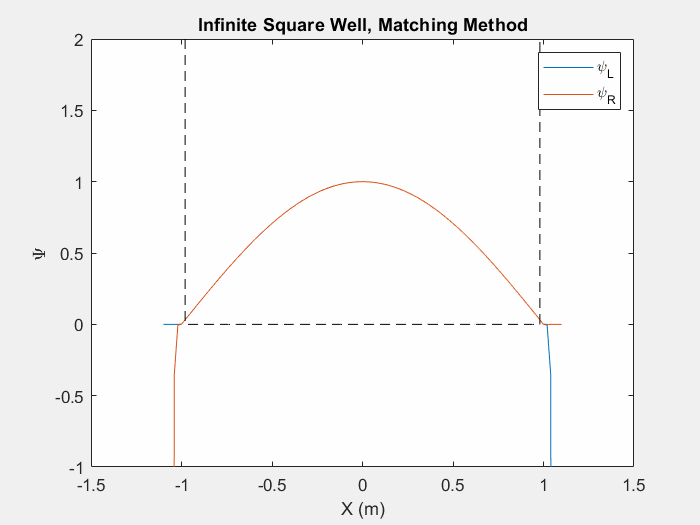
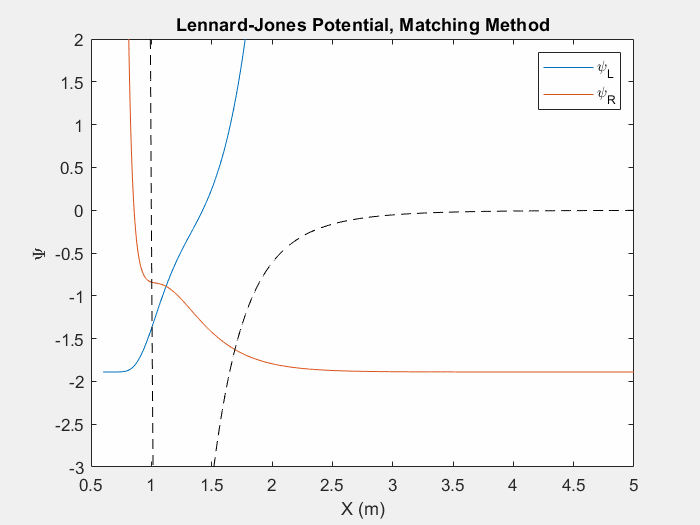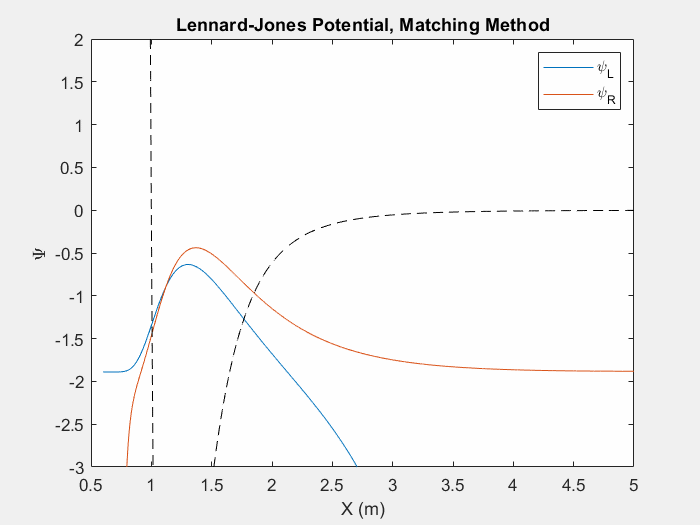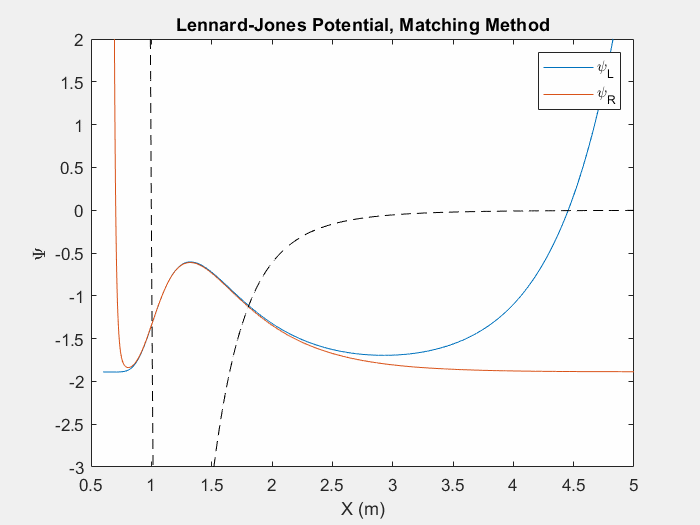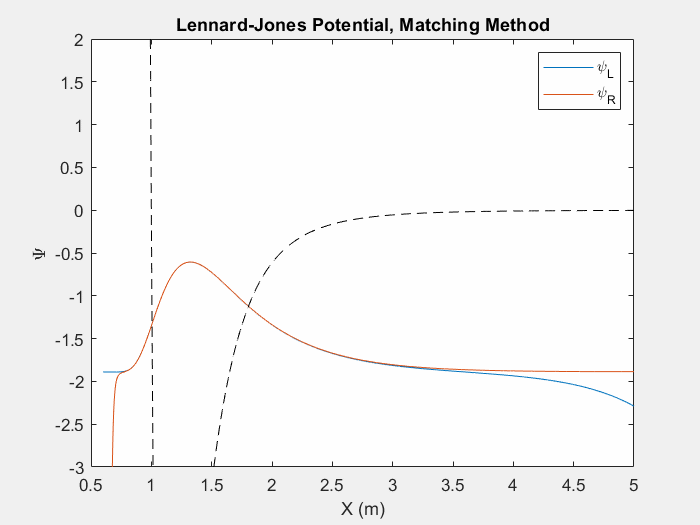
Now that we can calculate a wavefunction we must find the eigenenergies associated with a system in order to determine the eigenstate. There are multiple ways to do this, one such is the matching method which is particularly useful for asymmetric potential systems. The goal of the matching function is to generate a smooth and continuous wave function by combining two wavefunctions which are generated from the left and right corners of the potential array.

Figure (1) – Matching method inside an infinite square well.

The  inputs  of a matching method function are an initial energy guess, the potential array, the spatial step size, and an indexing point which we will use to check the slope of each wavefunction.  In order to calculate each wave function, there are unique initial conditions for even and odd parity solutions:

Using equation 3 and the initial conditions, we can calculate the first wavefunction using our initial energy guess. Then, we repeat this process by first flipping the potential array and generating a second wavefunction with the same initial conditions. We then flip this second wavefunction so that we have effectively generated one array from left to right and a second array from right to left. We then normalize each wavefunction at the indexed point so that they intersect.

Now we may calculate the slope of each wavefunction at the index. We then call a secondary matching function which keeps track of the orientation of the slopes. If each slope’s relative orientation remains the same, then our ‘change in energy’ value, which we will add afterwords, remains the same. If each slope’s relative orientation changes, then our ‘change in energy’ value is halved and negated. In either case, we then add a ‘change in energy’ value to the original energy guess, recalculate the left and right wavefunctions and repeat the process.

This function allows us to find eigenstates and hone in on the eigenenergies of a system. Once we reach a certain limit, the ‘change in energy’ value will be so small that we can stop the program and merge the two functions at the index point.

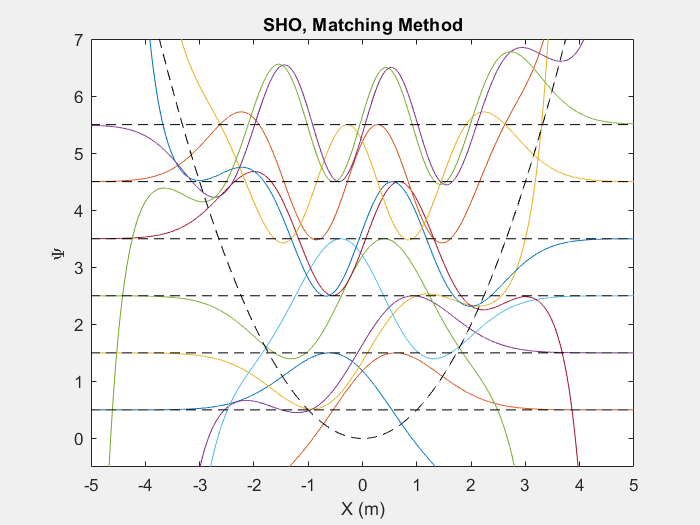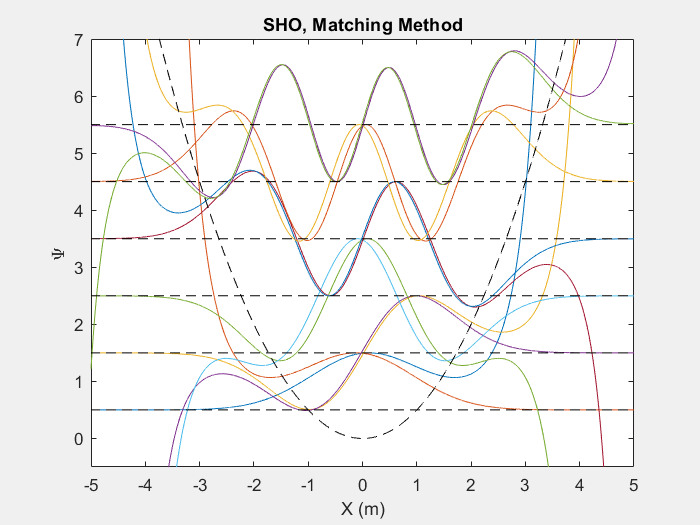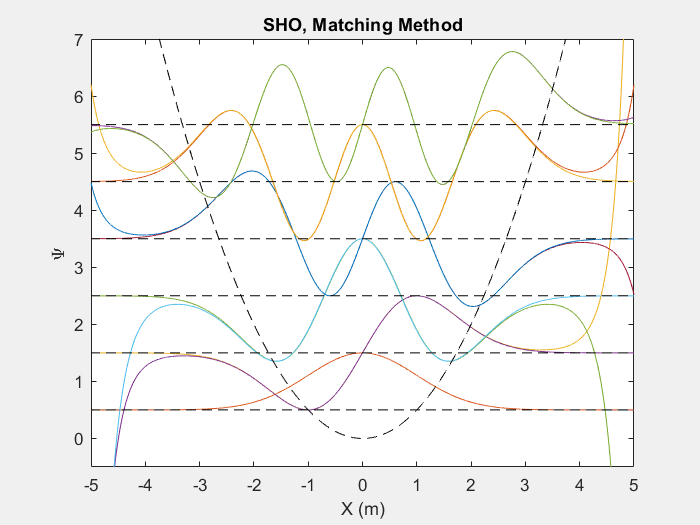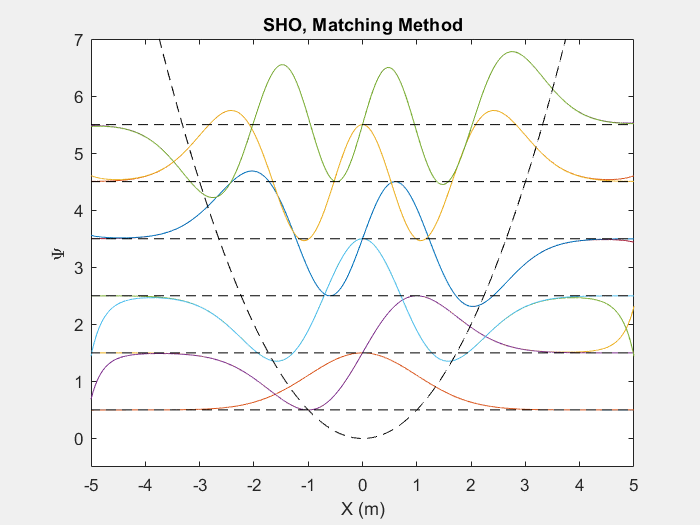
There are many useful applications of this method, one such is the quantum harmonic oscillator. The quantum harmonic oscillator is a useful analog for many arbitrary potentials which have stable equilibrium points.

Figure (2) – Top shows the matching method running on the first 6 energy levels of a quantum harmonic oscillator. Bottom shows the end result.

Figure (3) – The probability distribution of the 100th energy level as a result of the matching method.

Figure (4) – Another useful potential to study is the Lennard Jones potential. This potential is used to model the van der Waals forces between inert atoms.

Monte Carlo Method

Another useful computational method is the Monte Carlo method. Rather than guessing at the energy as in the matching method, in this method we will be guessing at the wavefunction and iterating on this guess. The idea of a Monte Carlo method is that we randomly change a system and only keep the changes that bring us closer to a solution we would expect. In the case of quantum mechanics, this will be used to randomly change the wavefunction and only keep the changes that lower the energy of the system.

In order to implement this approach, we must first understand how to calculate energy using equation 4 below:

In order to preform these integrals in discrete space, we can use several different methods, but for this process I chose to use the trapezoidal integration method:

Applying this method to the quotient and denominator of equation 4 leaves us with the following equations:

Now equation 4 becomes:

But now we have energy on both sides of the equation. In order to resolve this, we need to substitute in the time independent Schrödinger equation (Eq. 1) which gives us

Finally, in order to get rid of the double partial derivatives, we substitute in equation 2 and find:

This is the final solution which will allow us to calculate the energy in any system given a wavefunction and potential array.

Now that we can calculate energy, we can utilize the Monte Carlo method. This method is actually quite simple; we create a function that takes in an arbitrary guess of the wavefunction and calculate the energy of this guess. Then we randomly pick a point of the wavefunction and change it by a random amount. Then we recalculate the energy of the system and if the energy has decreased, we can keep that random change, otherwise discard the change and revert to the previous wavefunction. We repeat this process over and over again until we reach a point in which the energy does not change after a certain number of attempts. At this point we can assume the we reached the ground state of our potential system.

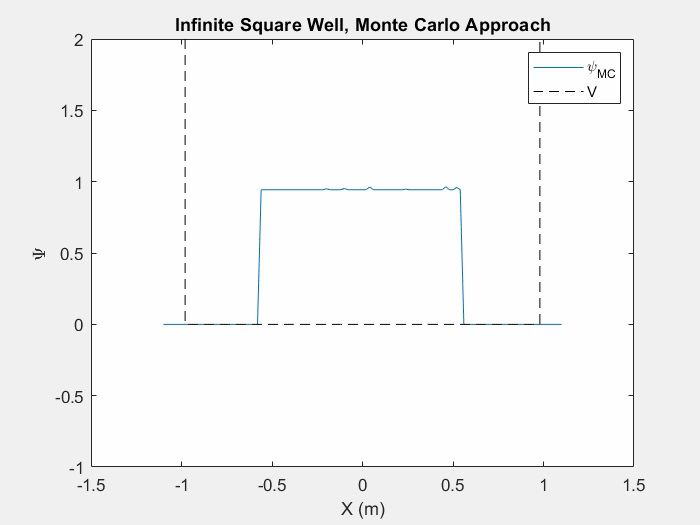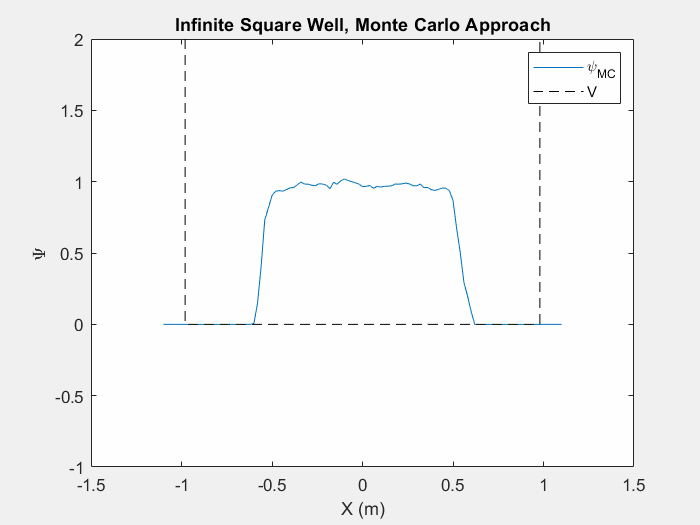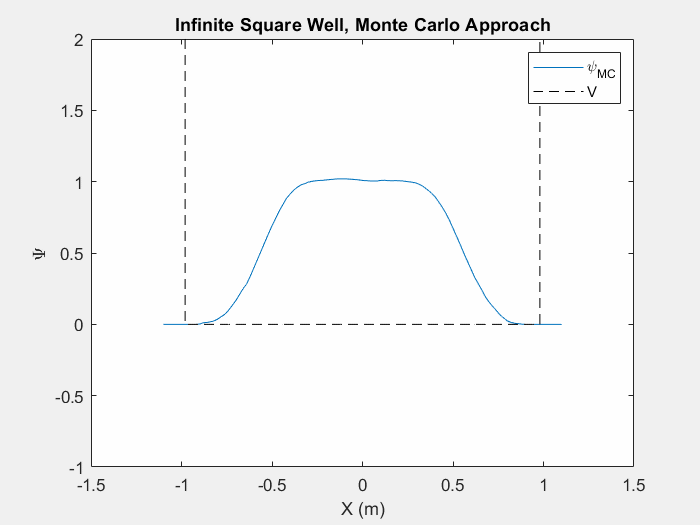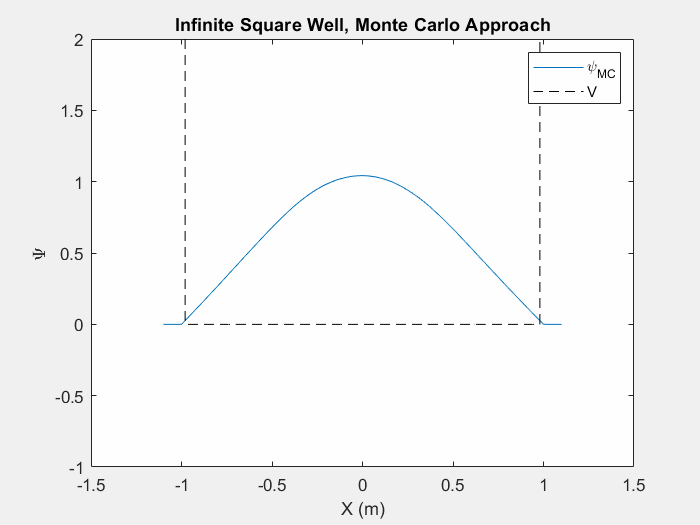
Figure (5) – The Monte Carlo method in an infinite square well. This animation takes place over ~5 million iterations.

Figure (6) – Monte Carlo method in a Lennard Jones potential. This animation takes place over ~50 million iterations.

Typically when using the Monte Carlo method on a new potential system, it is actually quite difficult in order to tell when we have reached the ground state unless we actually watch the iterations as they happen. As the wavefunction starts to change less and less we can assume that we are nearing the ground state.  This is still a very slow process and it can take vastly different times to reach the ground state depending on your initial wavefunction guess and the step size of your random changes.

While the Monte Carlo method is significantly slower than the matching method, it is still incredibly useful in finding the ground state energy of an arbitrary system. We typically need little to no intuition as to what the ground state looks like when we make our initial wavefunction guess. As long as the Monte Carlo method is run for a sufficient amount of time, the function will approach a ground state. Another downside of the Monte Carlo method is that it will only search for the ground state. The matching method, however, is useful in finding multiple energy levels. This method will resonate around any eigenstate as long as our initial energy guess and ‘change in energy’ value permits it. Overall, both functions have their applications and can be very useful in tandem.

As an aside, I should also say that both of these methods are only useful if we already understand how to describe the potential of a system and only seek the eigenenergies of said system. In the real world, most researchers are typically suffering from the inverse problem, in which we know the energies of the system but must use this information in order to construct a potential that coincides with these energies. While these methods may not be useful for those researchers, I still think these are valuable, especially to the student who wishes to study systems that we may already know how to describe.